Power Calculation for the Cochran-Mantel-Haenszel Test
Paul W. Egeler, M.S., GStat
2024-08-18
Source:vignettes/samplesizeCMH-power.Rmd
samplesizeCMH-power.RmdCalculating post hoc Power
The Data Set
We will use the Titanic dataset in
the datasets package to demonstrate a
post hoc power calculation. This dataset is explored in greater
detail in the introductory
vignette.
Let \(X\) = sex, \(Y\) = survival, and \(Z\) = class. Just as was performed in the introductory vignette, we will load the data and then create a set of partial tables stratified at fixed levels of class.
data(Titanic, package = "datasets")
partial_tables <- margin.table(Titanic, c(2, 4, 1))
ftable(partial_tables)## Class 1st 2nd 3rd Crew
## Sex Survived
## Male No 118 154 422 670
## Yes 62 25 88 192
## Female No 4 13 106 3
## Yes 141 93 90 20The Test Statistic
As we saw in the introductory vignette, performing a CMH test on the partial tables above shows that there is strong evidence that the common odds ratio is greater than one. This would indicate an association between sex and survival, even when accounting for the confounding class variable.
mantelhaen.test(partial_tables)##
## Mantel-Haenszel chi-squared test with continuity correction
##
## data: partial_tables
## Mantel-Haenszel X-squared = 360.33, df = 1, p-value < 2.2e-16
## alternative hypothesis: true common odds ratio is not equal to 1
## 95 percent confidence interval:
## 8.232629 14.185153
## sample estimates:
## common odds ratio
## 10.80653The Power Calculation
Now that we’ve established an association, we’ll use the power.cmh.test()
function to calculate the probability that our rejection of the null
hypothesis is a true result.
library(samplesizeCMH)
# Pre-computing counts (for readability)
column_props <- apply(partial_tables, 3, prop.table, 2)
props_male_survived_no <- column_props[1, ]
props_male_survived_yes <- column_props[3, ]
n_total_by_class <- apply(partial_tables, 3, sum)
n_total_by_class_survived_no <- apply(partial_tables[, 1, ], 2, sum)
n_total <- sum(Titanic)
power.cmh.test(
p1 = props_male_survived_no,
p2 = props_male_survived_yes,
N = n_total,
power = NULL,
s = n_total_by_class_survived_no / n_total_by_class,
t = n_total_by_class / n_total
)## NOTE: Effect size ('theta') is not consistent between strata.## Power and sample size calculation for the Cochran Mantel Haenszel test
##
## N = 2201
## Effective N = 2201
## Significance level = 0.05
## Power = 1
## Alternative = two.sided
##
## Number of subjects per each group:
## ______________________________________
## Group | 1 2 3 4
## ======================================
## Case | 122 167 528 673
## Control | 203 118 178 212
##
## CALL:
## power.cmh.test(p1 = props_male_survived_no, p2 = props_male_survived_yes,
## N = n_total, power = NULL, s = n_total_by_class_survived_no/n_total_by_class,
## t = n_total_by_class/n_total)Perhaps unsurprisingly, the power of this test approaches 100%.
Power and Effect Size in a Negative Result
It does not make sense to calculate power in a study when the null
hypothesis is not rejected. However, it may be of interest to the
researcher to determine the minimum effect size that could be detected,
given the sample size of the study and a specified power. We use the
example of the Nurses’ Health Study explored by Munoz and Rosner (1984). This study looked for a
link between oral contraceptives and breast cancer, stratified by age
(Barton et al. 1980; Hennekens et al.
1984). The data for this illustration has been included in the
samplesizeCMH package.
## Age Group <= 34 35 - 39 40 - 44 45 - 49 50 - 55
## OC Usage Disease Status
## Exposed Case 31 57 69 86 30
## Control 363 521 760 725 272
## Not Exposed Case 40 107 196 241 132
## Control 327 1146 1914 2503 1370Here, as shown in Hennekens et al. (1984), the Mantel-Haenszel test shows non-significant results, with the common odds ratio approximately equal to 1.
mantelhaen.test(contraceptives)##
## Mantel-Haenszel chi-squared test with continuity correction
##
## data: contraceptives
## Mantel-Haenszel X-squared = 0.33106, df = 1, p-value = 0.565
## alternative hypothesis: true common odds ratio is not equal to 1
## 95 percent confidence interval:
## 0.902928 1.214722
## sample estimates:
## common odds ratio
## 1.047285The question now is what effect size would be detectable if an effect truly did exist in the data. That is to say, what effect size were we prepared to correctly detect given our data and specified significance level and power? We can test a wide range of effect sizes to see where the effect size crosses over into adequate power.
To accomplish this, we will partially apply the power.cmh.test()
function and then vectorize it over theta. Passing in a
vector of thetas to the new function will provide us with a vector of
computed powers. Although a simple for() loop would
suffice to generate a power curve, there is an additional benefit
associated with the creation of a partially applied function—we will see
later how it can be used to compute the exact effect size that will
yield 90% power.
n_control_exposed <- contraceptives[1, 2, ]
n_control_total <- apply(contraceptives[, 2, ], 2, sum)
n_total_by_age <- apply(contraceptives, 3, sum)
n_total <- sum(contraceptives)
partial_power_func <- function(theta) {
power.cmh.test(
theta = theta,
p2 = n_control_exposed / n_control_total,
N = n_total,
power = NULL,
s = 1/11,
t = n_total_by_age / n_total,
alternative = "greater"
)[["power"]]
}
vectorized_power_func <- Vectorize(partial_power_func, "theta", SIMPLIFY = TRUE)Using the function above, we may create a power curve.
thetas <- seq(1.05, 1.5, 0.05)
powers <- vectorized_power_func(thetas)
plot(y = powers, x = thetas, main = "Power curve as a function of effect size")
abline(h = 0.95, col = "gold")
abline(h = 0.90, col = "red")
abline(h = 0.80, col = "blue")
legend(
"bottomright",
legend = c("95%", "90%", "80%"),
col = c("gold", "red", "blue"),
bty = "n",
lty = 1L,
title = "Power level"
)
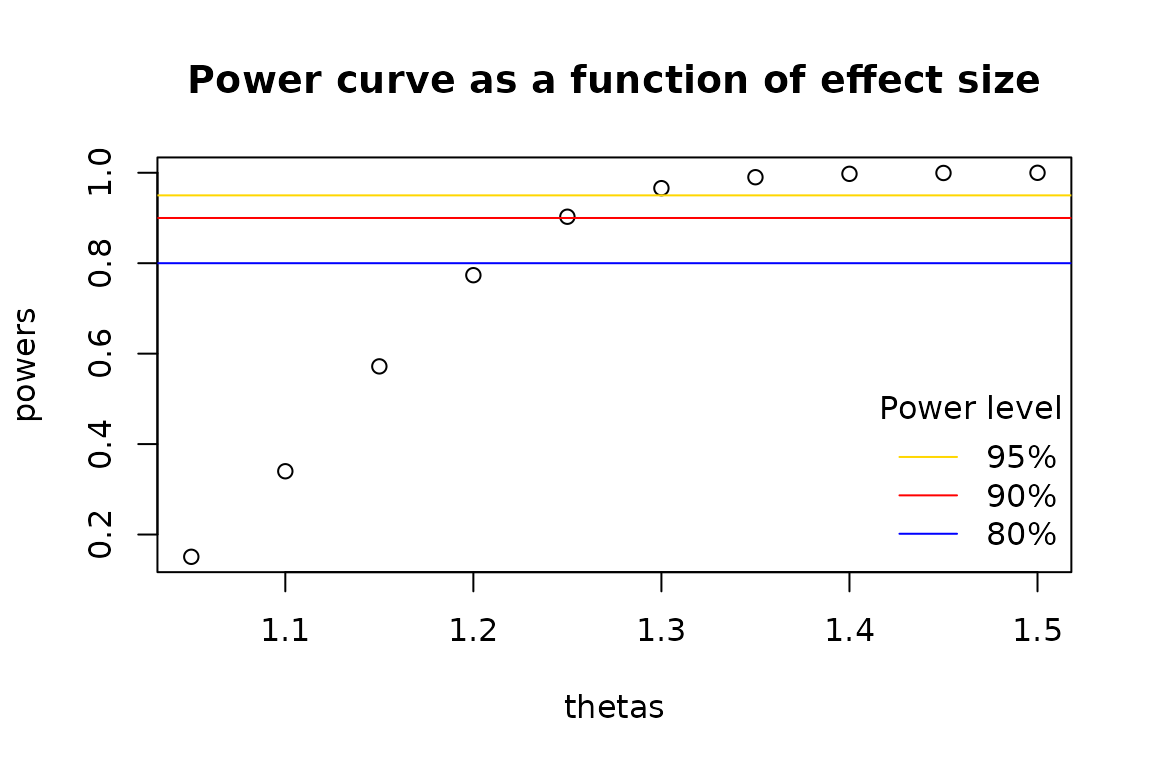
As we can see from above, 90% power would have been achieved if the
common odds ratio was estimated to be approximately 1.25. To compute the
exact effect size, we employ the stats::uniroot()
function.
target_power <- 0.90
first_over <- which.min(powers <= target_power)
interval <- thetas[c(first_over - 1, first_over)]
uniroot(function(theta) partial_power_func(theta) - target_power, interval)$root## [1] 1.248515